Investing Math Matters

關乎收益的投資數學

by Charles Cheng, CFA
鄭又銓, CFA

 

 

The math of investing returns is something easily overlooked or misunderstood for the average investor. But even simple differences in calculation or understanding can make all the difference when making investment plans.

投資回報的數學是普通投資者容易忽視或誤解的。但即使是簡單的計算或理解差異，在製定投資計劃時也會產生重大影響。

 

 

One of the fundamental concepts in finance is compound interest. There is an apocryphal quote attributed to Albert Einstein where he jokes that compound interest is the most powerful force in the universe. The significance is that over long periods of time, compounding returns at different rates or times leads to large differences in wealth. It’s hard to get a sense of the magnitude of the differences unless you actually do the calculations.

金融中的一個基本概念是複利。有一個偽愛因斯坦引文，說他曾開玩笑說，複利是宇宙中最強大的力量。重要的是，在很長一段時間內，以不同的利率或時間複合的回報能產生財富的巨大差異。如果你進行實際的計算，就會發現其中差異的大小。

 

 

As seen in the chart below, starting to save 10 years earlier can mean almost double the wealth after 20-30 years despite only putting in 33% more money in total.

如下圖所示，儘管只增加了33％的資金，但是若提前10年開始儲蓄可能意味著20至30年後財富幾乎多了一倍。

 

Compound interest- Saving $200 per month at 6% starting at age 25 vs 35

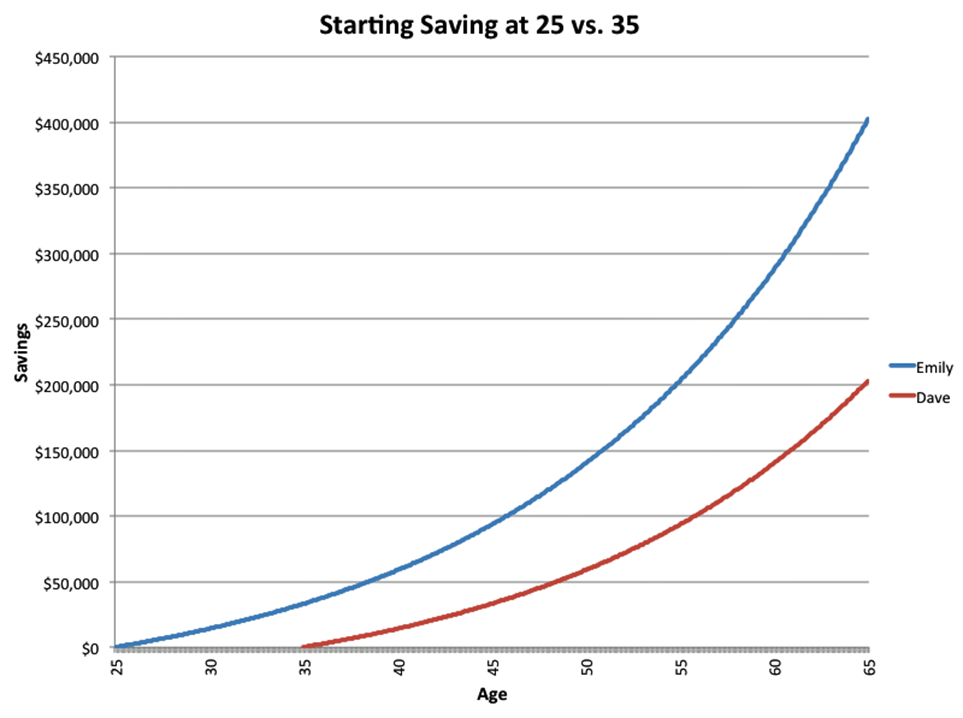
Source: Business Insider. Saving $200 per month at 6%.

來源：商業內幕期刊，每月省下200元以6%的複利增長

 

 

Source: Business Insider

來源：商業內幕期刊

 

This effect also dramatically changes the amount needed to be saved each in order to reach a return target. One would need to save almost four times more per month at age 40 vs age 20. Also, even small differences in return can make big differences when compounded over many years. A single lump sum of $10000 will grow to almost $150,000 after 40 years at 7% compounded returns vs around $70,000 at 6%.

此複利效果還會顯著改變為了達到收益目標而需要的存款數額。如果從40歲開始存錢，那麼他相對於20歲開始的人他需每月多存4倍的錢才能達到相同的收益目標。此外，即使很小的回報差異在經過多年複合後也會產生很大的差異。單筆10000美元，若以複利7%的利率增長，那麼在40年後將增長至近150,000美元，而若以6％的複利增長，在40年後則僅得到70,000美元左右。

 

 

The math for calculating return itself is actually not very straightforward. One 6% average return can be worse than another 6% average return. How is this possible? Because average returns can be either arithmetic or geometric averages. For example, if an annual return series is 6% in year one, and -4%, 2%, and 12% in year two to four, the arithmetic mean is (16%-15%+22%-3%)/4 = 5%. The geometric mean is (1.16)(0.85)(1.22)(.97)^(1/4) = 3.9%, a lower return, but one which more accurately represents the annual compounded rate that results in the actual total return of 16.7%.

計算回報本身的數學實際上並不是非常直觀。一個6%的平均回報率有時表現會劣於另一個6%的平均回報率。這是怎麼回事？因為平均回報可以是算術平均值或幾何平均值。例如，如果第一年的年回報率為6％，接下來三年的回報率為-4％，2％和12％，則算術平均值為(16%-15%+22%-3%)/4 = 5%，幾何平均值為(1.16)(0.85)(1.22)(.97)^(1/4) = 3.9%。後者回報較低，但卻是更準確地顯示得到4年總回報16.7%的複利率。

 

 

An even more extreme example is as follows. Above are two hypothetical return series. Investor A receives 30% for four years followed by losing -60% every 5^th year. Investor B receives +12% every four years followed by losing -10% every 5^th year. Which return would give you more money over time? Many people would choose A, as it appears that the total percentage would be higher. Indeed, the arithmetic average return is higher at 12% vs 8% for investor B. However, the reverse is true.

更極端的例子如下。以上是兩組假設的收益組。投資者A四年收益率為30％，之後每個第五年跌60％。投資者B每連續四年收益+12％，然後每第五年跌10％。隨著時間的推移，哪個模式會帶給你更多收益？許多人會選擇A，因為看起來總百分比會更高。確實，投資者A的算術平均收益率為12％，高於投資者B的8％。但事實恰恰相反。

 

 

Investor B (Grey) vs Investor A (Blue)

 

After a period of 30-40 years, the returns to Investor B far outpace those to Investor A. It is also much less volatile, making it even more attractive as an investment. Indeed, it is because of its high volatility that investment A does not have as high a geometric return and ending value as investment B. Investing is often described as being a tradeoff between risk and return. In this case, and in some real-life investing decisions, understanding the math and nature of investment returns can help you have both higher returns and lower risk.

經過30到40年的時間，投資者B的回報遠遠超過了投資者A。它的波動性也比投資者A的低許多。作為一項投資，B的模式更具吸引力。實際上，正是由於其高波動性，投資A的幾何平均回報和總投資回報都不如投資B。投資通常被描述為風險和收益之間的權衡。在上述的例子中，以及在一些現實生活中的投資決策中，了解投資回報的數學和性質卻可以幫助您同時獲得更高的回報和更低的風險。

 

 

Mr. Cheng is a managing partner at a Hong Kong based independent private investment office. This article reflects his personal views and not his firm’s and should not be viewed as an investment recommendation.

鄭先生為可承資本，一家總部設於香港的獨立投資辦公室之董事合夥人。這篇文章反映了他的個人而非公司觀點。該文章不應被視為投資建議。

 

 

 

 

 

---